According to legend, an Emperor of ancient Vietnam, looking for someone to occupy the position of wiseperson, created a problem to test the ability of such a candidate. The problem consists of a number of disks and three rods: I, the source, II, the spare, and III, the destination. Disks of different sizes have holes in the middle so they can fit on the rods. Because of their great weight, disks can only be placed on top of disks larger than themselves. Initially, all the disks are on the rod of Tower I. The problem is to move the disks, one by one, from the rod of Tower I to the rod of Tower III using the rod of Tower II. Many lengthy and complicated solutions were offered to the Emperor who was convinced that there was an easy solution to the problem. And there was.
A great Buddhist monk from the mountains, proclaiming that the problem almost solves itself, offered the following solution. If there is only one disk (that is, N = 1), move it from rod I to rod III. If there is more than one disk, do the following:
- Ignore the bottom disk and solve the problem for N – 1 disks, using rod II as the destination, and rod III as the spare.
- After this, N – 1 disks will be on rod II, and the largest will remain on rod I. Solve the problem for N = 1 by moving the large disk from rod I to rod III.
- Move the N – 1 disks from rod II to rod III. That is, solve the problem with rod II as the source, rod I as the spare, and rod III as the destination.
After a period of silence, the confused Emperor asked whether the monk was going to tell his solution. The monk smiled omnisciently and vanished.
The patterns of movement in the solution require the minimum number of movements to solve the problem. The solution is recursive, and is the basis for the graphic presentation.
To download or save the software, click on the icon below or on the icon on the previous page. The program was designed for screen resolution 1024×768
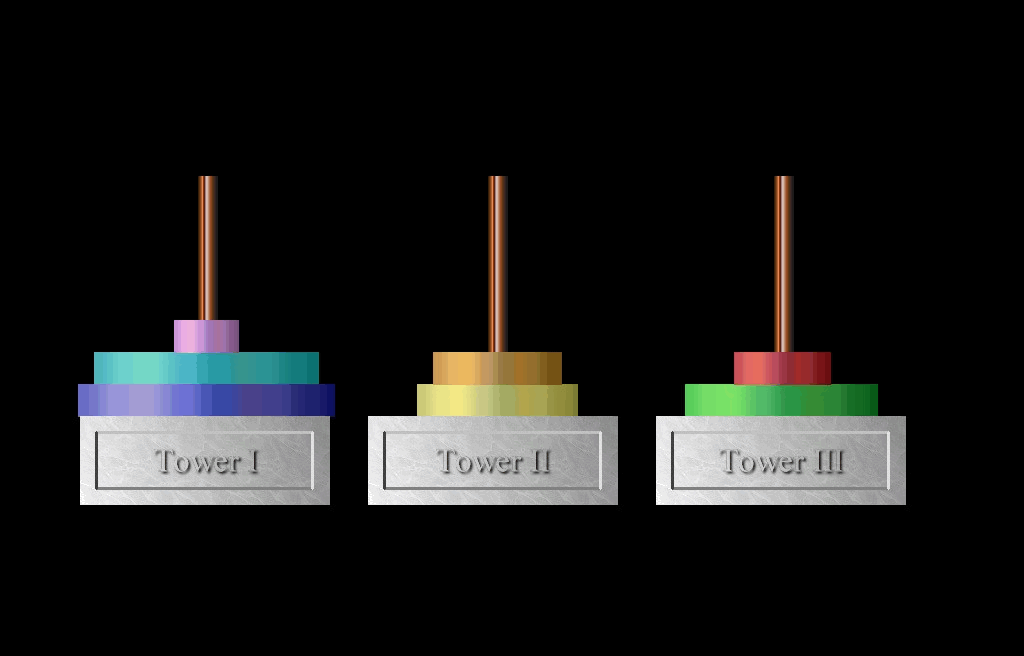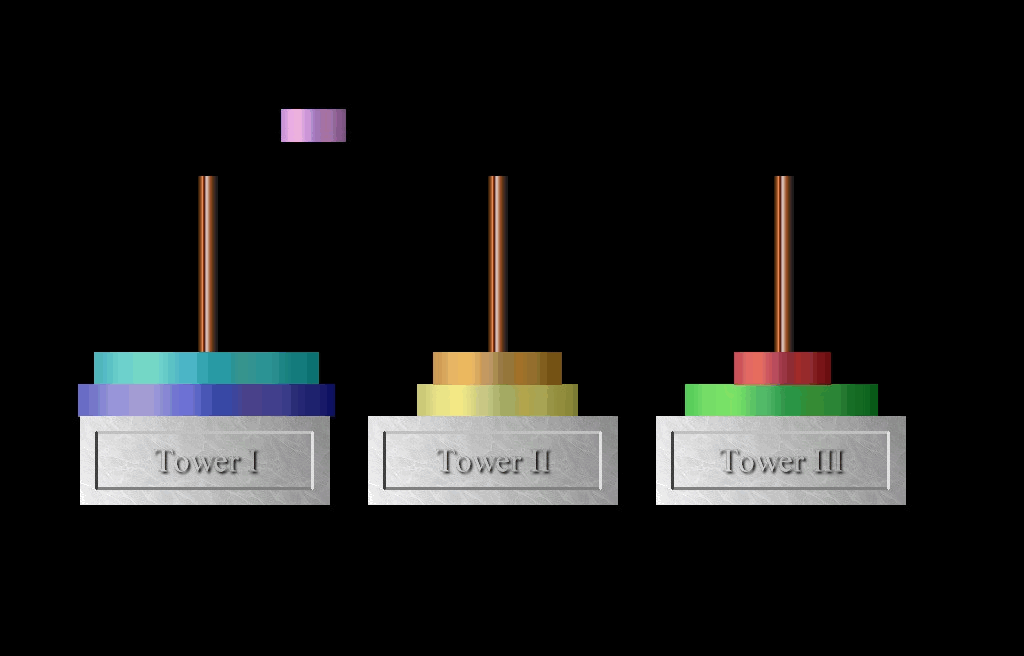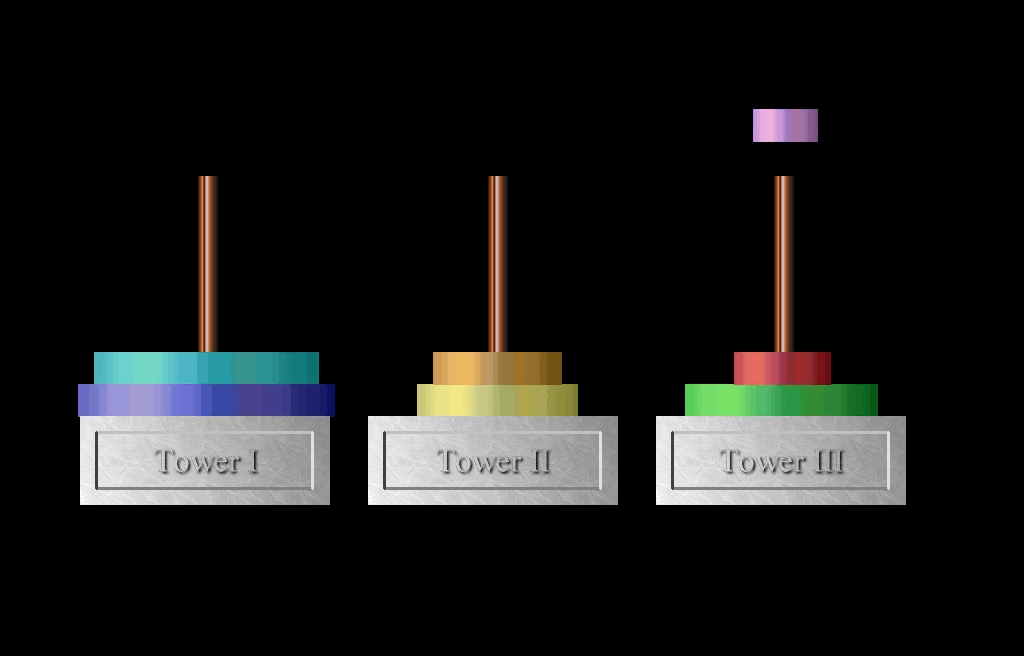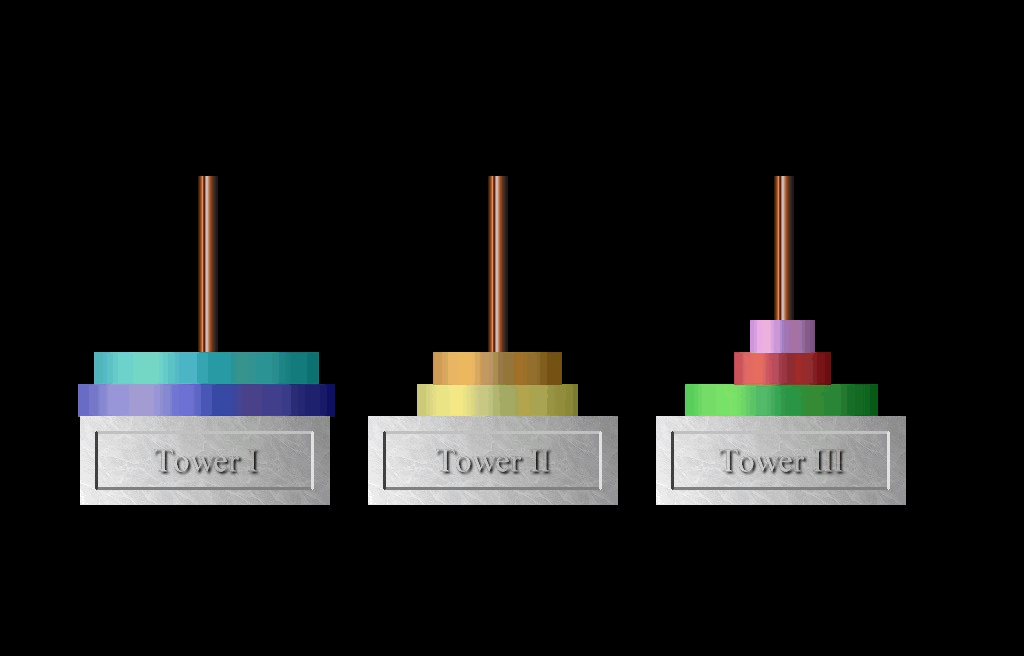
According to legend, an Emperor of ancient Vietnam, looking for someone to occupy the position of wiseperson, created a problem to test the ability of such a candidate. The problem consists of a number of disks and three rods: I, the source, II, the spare, and III, the destination. Disks of different sizes have holes in the middle so they can fit on the rods. Because of their great weight, disks can only be placed on top of disks larger than themselves. Initially, all the disks are on the rod of Tower I. The problem is to move the disks, one by one, from the rod of Tower I to the rod of Tower III using the rod of Tower II. Many lengthy and complicated solutions were offered to the Emperor who was convinced that there was an easy solution to the problem. And there was.
A great Buddhist monk from the mountains, proclaiming that the problem almost solves itself, offered the following solution. If there is only one disk (that is, N = 1), move it from rod I to rod III. If there is more than one disk, do the following:
- Ignore the bottom disk and solve the problem for N – 1 disks, using rod II as the destination, and rod III as the spare.
- After this, N – 1 disks will be on rod II, and the largest will remain on rod I. Solve the problem for N = 1 by moving the large disk from rod I to rod III.
- Move the N – 1 disks from rod II to rod III. That is, solve the problem with rod II as the source, rod I as the spare, and rod III as the destination.
After a period of silence, the confused Emperor asked whether the monk was going to tell his solution. The monk smiled omnisciently and vanished.
The patterns of movement in the solution require the minimum number of movements to solve the problem. The solution is recursive, and is the basis for the graphic presentation.
To download or save the software, click on the icon below or on the icon on the previous page. The program was designed for screen resolution 1024×768
